Thoughts on Surfboard Volume, Rider Weight, and Paddling Speed (part 1)

Let's examine the interaction between board volume, rider weight, and paddling speed. I'm going to do a few calculations, but first lets make some assumptions:

1. Assume people are the same density as water. This is pretty close to true. I Googled a study that said people are generally lighter than water with a full breath of air, and heavier than water with no air in their lungs. This implies that they're the same density at water with a partial breath. This should be close enough.

2. Assume a person's volume is distributed similarly to a block representing a torso, and a wedge representing legs. This is a bit of a stretch, but it's required to do some approximation to do our calculations. Hopefully this is close enough. Person number 1 is illustrated below, and is based on some measurements I took of myself. I am about 14" wide (excluding my arms) and 10" thick in the torso. I weigh about 165lbs, which is 75 kilograms, and as such, displace 75 liters of water. Figure 1 below is person 1.

3. Assume salt water is equally as dense as fresh water, so we can do easy conversions between kg and liters. In reality, salt water is about 2.5% heavier than freshwater, but this varies depending on where you are in the world (some oceans are saltier than others).

Figure 1

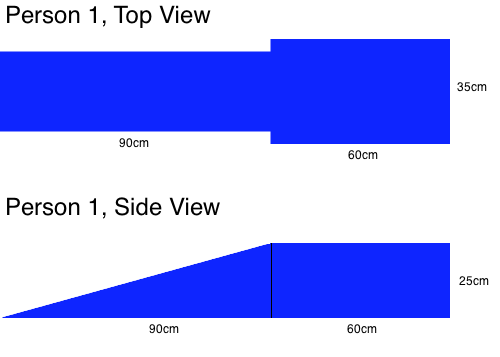
Surfboard 1 is a 6'0"x18"x2 3/8" pro-style shortboard. It has a volume of 26.8 liters. This is a number I came up with designing such a board in Aku Shaper, which is the surfboard design software I use. We'll assume this board weighs 3kg, which is about 6.5 pounds.

So, when person 1 paddles around on board 1, he lies down and looks (vaguely) like the illustration above. He weighs 75kg, he's on a board that weighs 3kg, and he's got 26.8l of flotation to work with. Since the board weighs 3kg, it uses it's first three liters of displacement just to float itself. That leaves 23.8l to float our surfer. He'll sink lower and lower into the water until exactly 23.8l of his own volume is still above the surface. The part of him that's below water doesn't have any effect -- it floats itself, but no more than itself, because, based on our earlier assumption, people have exactly the same density as water.

So, while person 1 is paddling around on surfboard 1, what does that look like below the water? First, we need to know how much of our surfer is under water. Let's do a little calculation here -- we need to be able to calculate the height of the part of our guy that's above water based on a known volume, which is the portion of our surfboard that's not being used to float itself (the leftover 23.8l).

For the block portion of our surfer:

    V = length * width * height

so:

    V = 60 * 35 *h

And for the wedge portion:

    V = (length * width * height) / 2
    V = (3.6h * 20 * h)/2
    V = (3.6h^2 * 20)/2

So for the whole surfer:

    V = 36 * h^2 + 2100 * h

But we already know V, what we want to find is h. We can do this with the quadratic equation.

First we put our equation into standard ax^2 + bx + c = 0 format:

    36*h^2 + 2100*h +(-V) = 0

Then we stick all our numbers into the quadratic equation:

    h = (-2100 +/- sqrt(2100^2 - 4 * 36 * (-V))/(2*36)

Since the quadratic equation actually gives two possible solutions, we'll look at both:

    h = (-sqrt(4410000 - 144*(-V)) - 2100)/72

or:

    h = (sqrt(4410000 - 144*(-V)) - 2100)/72

We can test both of these, because we know that h should come out to 25 when V is 75,000 (it's not 75, because all our numbers are in centimeters, not meters, so we'll work in milliliters to match).

When we plug in 75,000 to both equations:

    (-sqrt(4410000 - 144*(-V)) - 2100)/72 = -83.3333
    (sqrt(4410000 - 144*(-V)) - 2100)/72 = 25

Obviously, the second one is the right answer.

So our final formula is:

    h = (sqrt(4410000 - 144*(-V)) - 2100)/72

Where h is the height of the above water portion of our surfer, and V is the volume of the above water portion of our surfer, in ml.

So, back to the problem at hand. We're floating 23.8l of surfer above the water. We need to find that height:

    h = (sqrt(4410000 - 144*(-23800)) - 2100)/72
    h = 9.71

Since our surfer's whole height is 25, about 15cm of him is below water (25 - 9.71). What implication does this have for how our board is floating? Well, when we paddle, we keep the nose of our board just above the water's surface, right?

Consider the Following Illustration

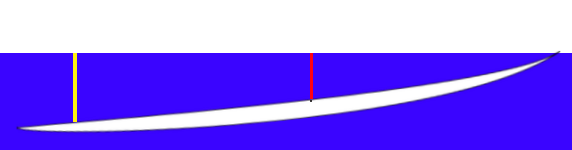
The red line indicates water depth at the chest. It's set to match our 15cm depth we calculated. The board is rotated around that spot to try and match the angle we hold our boards at when we paddle -- that is, with the nose just above the surface.

Looking at some photos of surfers paddling, it seems the backs of their knees are normally under water while paddling around on shortboards. Based on measurements of myself, that puts the water at about 8" (20cm) deep (over their boards) at their knees. This should be roughly 8" (20cm) from the tail of their boards (based on one of my own boards and where my knees are positioned over it). The yellow line on the drawing indicates depth at the knee. This works out to 23cm in the drawing, or about 9". This is slightly higher than my guess based on photos, but in the same ballpark. Possibly people float in a bit different position than I've estimated based on my block/wedge person and my chest-depth line, or possibly most people in my photos aren't surfing boards as small as the pros, so they sit a bit higher in the water.

But now look at that board. Look at the angle it sits at in the water. The lowest point of the board in the water is about 27cm deep, or about 10.6". Since our board is 18" wide, we can determine the approximate frontal area of this board and surfer in the water (10.6*18) and it works out to be about 191 square inches. That's all drag that the surfer has to deal with when he's paddling.

Now, consider replacing the surfboard with a floatier model. If we adjust the board so that it's 19 1/2" wide, and 2 5/8" thick (but still 6'0"), we've now got a board with a volume of 31.74 liters. We can assume the board weighs the same as the slightly smaller board. Almost all the added volume is foam, and foam doesn't weigh much.

If we redo our calculations, we subtract 3 liters so the board floats itself, and are left with 28.74l to float our surfer. We plug that into our equation to try to find the height of the surfer above water:

    h = (sqrt(4410000 - 144*(-28740)) - 2100)/72
    h = 11.44

We subtract this from our 25 and get about 13.5cm of depth now, instead of the 15 from before. Let's make a new drawing based on that. Also note our board is 1/4" thicker, so it will be slightly lower in the water just because of that.

Here's the New Drawing

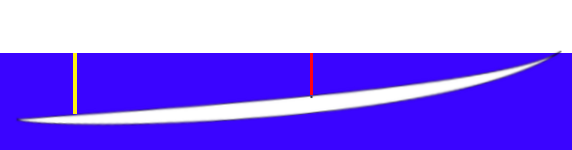
We've adjusted the depth of our red line based on 13.5cm + 1/4" for the extra board thickness. Now we don't have to push the tail of the board as low in the water. In fact, the yellow line works out to just over 20cm, or about 8" this time. The deepest spot on the bottom of our board is now around 24cm, or about 9.4". With our new, wider board, our new frontal surface area is 9.4*19.4 = 183 square inches.

This works out about 4% less area, which presumably means 4% less drag (drag calculations are complicated and this is a gross oversimplification). That's not as big a number as I was expecting. Maybe you paddle 4% faster on the bigger board than the smaller one? Is that enough to make the extra foam worth it? Maybe not. This is also the improvement coming from a board with 18% more volume than the smaller one.

The Previous Two Drawings Overlaid On Top Of One Another

Interesting Follow-Up Experiments

1) Put a surfer in a pool with a high-volume and low-volume shortboard of the same length. Measure the actual draft of each board. See how much difference there is.

2) In the same pool, on each of the boards, have him do paddle sprints. Make each one a short distance (say, 20 yards) and time them. Alternate boards each time, and average the times for each board at the end. See how much faster he actually paddles on the floatier board. I choose to do short sprints here because it more accurately represents trying to catch a wave than doing long-distance paddling.

Updates

1. 2011-03-19 How Much Surfboard Do You Really Need?
2. 2010-09-23 Thoughts on Volume, Weight, and Paddling 2
3. 2010-09-21 Thoughts on Volume, Weight, and Paddling